Pengertian Algoritma
Algoritma
Dalam matematika dan ilmu komputer, algoritma adalah prosedur langkah-demi-langkah untuk penghitungan. Algoritma digunakan untukpenghitungan, pemrosesan data, dan penalaran otomatis.
Algoritma adalah metode efektif diekspresikan sebagai rangkaian terbatas [1] dari instruksi-instruksi yang telah didefinisikan dengan baik[2] untuk menghitung sebuah fungsi. [3] Dimulai dari sebuah kondisi awal dan input awal (mungkin kosong), [4] instruksi-instruksi tersebut menjelaskan sebuah komputasi yang, bila dieksekusi, diproses lewat sejumlah urutan kondisi terbatas [5] yang terdefinisi dengan baik, yang pada akhirnya menghasilkan "keluaran" [6] dan berhenti di kondisi akhir. Transisi dari satu kondisi ke kondisi selanjutnya tidak harusdeterministik; beberapa algoritma, dikenal dengan algoritma pengacakan, menggunakan masukan acak. [7]
Walaupun algorism-nya al-Khawarizmi dirujuk sebagai aturan-aturan melakukan aritmatika menggunakan bilangan Hindu-Arab dan solusi sistematis dan persamaan kuadrat, sebagian formalisasi yang nantinya menjadi algoritma modern dimulai dengan usaha untuk memecahkan permasalahan keputusan (Entscheidungsproblem) yang diajukan oleh David Hilbert pada tahun 1928. Formalisasi selanjutnya dilihat sebagai usaha untuk menentukan "penghitungan efektif" [8] atau "metode efektif"; [9] formalisasi tersebut mengikutkanGodel-Herbrand-Kleene fungsi rekursif-nya Kurt Godel - Jacques Herbrand - Stephen Cole Kleene pada tahun 1930, 1934, dan 1935,kalkulus lambda-nya Alonzo Church pada tahun 1936, "Formulasi 1"-nya Emil Post pada tahun 1936, dan Mesin Turing-nya Alan Turingpada tahun 1936-7 dan 1939. Dari definisi formal dari algoritma di atas, berkaitan dengan konsep intuituf, masih tetap ada masalah yang menantang. [10]
Asal kata[sunting | sunting sumber]
'Algoritma' muncul dari 'Algoritmi', bentuk Latin dari al-Khwarizmi, matematikawan, ahli astronomi, dan ahli geografi dari Persia. [11][12]
Definisi informal[sunting | sunting sumber]
Definisi informalnya bisa berarti "sekumpulan aturan yang secara tepat menentukan seurutan operasi". [13] yang mengikutkan semua program komputer, termasuk program yang tidak melakukan perhitungan numerik. Secara umum, sebuah program hanyalah sebuah algoritma jika ia akan berhenti nantinya. [14]
Sebuah contoh prototipikal dari suatu algoritma adalah algoritma Euclid untuk menentukan bilangan pembagi terbesar dari dua integer; sebagai contohnya (ada contoh yang lain) dijelaskan dengan diagram alur di atas dan sebagai contoh di bagian lanjut.
Boolos & Jeffrey (1974, 1999) memberikan sebuah makna informal dari kata algoritma dalam persamaan berikut:
Tidak ada manusia yang dapat menulis begitu cepat, atau begitu lama, atau begitu kecil ("kecil, dan lebih kecil tanpa batas ... anda mungkin mencoba menulis di atas molekul, atom, elektron") untuk mencatat semua anggota dari kumpulan bilangan tak terbatas dengan menuliskan namanya, bergantian, dalam suatu notasi. Tapi manusia bisa melakukan sesuatu yang sama bergunanya, pada kasus kumpulan bilangan tak terbatas: Mereka dapat memberikan instruksi jelas untuk menentukan anggota ke-n dari set, untuk n terbatas acak. Instruksi tersebut diberikan secara eksplisit, dalam bentuk yang dapat diikuti oleh mesin penghitung, atau oleh manusia yang mampu melakukan hanya operasi-operasi dasar dengan simbol-simbol. [15]
Suatu "bilangan tak-terbatas" adalah bilangan yang elemen-elemenya bisa berkorespondensi satu-ke-satu dengan integer. Maka, Boolos dan Jeffrey mengatakan bahwa sebuah algoritma berarti instruksi bagi sebuah proses yang "membuat" keluaran integer dari sebuah "masukan" acak integer yang, secara teori, bisa sangat besar. Maka sebuah algoritma dapat berupa persamaan aljabar seperti y = m + n -- dua variabel masukan m dan n yang menghasikan keluaran y. Tapi berbagai penulis yang mencoba mendefinisikan persamaan tersebut mengatakan bahwa kata algoritma mengandung lebih dari itu, sesuatu yang kurang lebih (untuk contoh penjumlahan):
- Instruksi rinci dan tepat (dalam bahasa yang dipahami oleh "komputer") [16] untuk proses yang cepat, efisien, "baik" [17] yang menentukan "pergerakan" dari "komputer" (mesin atau manusia, dibekali dengan informasi dan kemampuan internal yang dibutuhkan) [18] untuk menemukan, dekode, dan kemudian mengolah masukan integer/simbolm dan n, simbol + dan = ... dan "secara efektif" [19] menghasilkan, dalam waktu yang "masuk akal", [20] keluaran integer y pada tempat dan format tertentu.
Konsep dari algoritma juga digunakan untuk mendefinisikan notasi dari desidabilitas. Notasi tersebut adalah pusat untuk menjelaskan bagaimana sistem formal berasal dari sejumlah kecil aksioma dan aturan. Dalam logika, waktu dari sebuah algoritma untuk selesai tidak dapat dihitung, karena tidak berelasi dengan dimensi fisik kita. Dari ketidakpastian tersebut, yang mengkarakteristikan pekerjaan yang sedang berjalan, timbulah ketidak-tersediannya definisi algoritma yang sesuai dengan konkrit (pada tingkat tertentu) dan penggunaan secara abstrak dari istilah tersebut.
Formalisasi[sunting | sunting sumber]
Algoritma sangat penting bagi cara komputer mengolah data. Banyak program komputer mengandung algoritma memberikan rincian pada instruksi khusus yang komputer harus lakukan (dengan urutan tertentu) untuk menjalankan pekerjaan tertentu, seperti menghitung gaji karyawan atau mencetak kartu rapor siswa. Maka, sebuah algoritma bisa dianggap sebagai urutan operasi yang bisa disimulasikan oleh sebuah sistem Turing-lengkap. Penulis yang mendukung tesis ini termasuk Minsky (1967), Savage (1987), dan Gurevich (2000):
Minsky: "Tapi kita juga menjaga, dengan Turing ... bahwa setiap prosedur yang "secara alami" disebut efektif, bisa dinyatakan oleh mesin (sederhana). Walaupun tampaknya ekstrim, alasan tersebut ... sukar disanggah". [21]
Gurevich: "... argumen informal Turing untuk menyokong tesis ini membenarkan tesis yang lebih kuat: setiap algoritma bisa disimulasikan oleh sebuah mesin Turing ... menurut Savage [1987], sebuah algoritma adalah sebuah proses penghitungan yang ditentukan oleh sebuah mesin Turing". [22]
Biasanya, bila sebuah algoritma dihubungkan dengan pengolahan informasi, data dibaca dari sumber masukan, ditulis ke perangkat keluaran, dan/atau disimpan untuk pengolahan selanjutnya. Data simpanan dianggap sebagai bagian dari keadaan internal dari entitas yang melakukan algoritma. Pada prakteknya, keadaan tersebut disimpan pada satu atau lebih struktur data.
Untuk beberapa proses komputasi, algoritma harus ditentukan secara teliti: dijabarkan dengan cara ia bakal berlaku untuk semua kemungkinan yang dapat timbul. Yaitu, setiap langkah tambahan harus secara sistematis dihadapi, kasus-per-kasus; Kriteria bagi setiap kasus harus jelas (dan bisa dihitung).
Karena sebuah algoritma adalah kumpulan dari langkah-langkah yang tepat, urutan dari komputasi selalu penting bagi berfungsinya algoritma. Instruksi biasanya diasumsikan terdaftar secara eksplisit, dan dijelaskan dimulai "dari atas" dan terus "ke bawah", sebuah gambaran yang dijelaskan secara formal oleh alur kontrol
Sejauh ini, diskusi tentang formalisasi algoritma telah mengasumsikan premis dari pemrograman imperatif. Hal ini merupakan konsepsi umum, yang mencoba menjelaskan sebuah pekerjaan dalam makna diskrit dan "mekanis". Keunikan dari konsepsi formalisasi algoritma adalah operasi penetapan, mengatur nilai dari sebuah variabel. Ia berasal dari intuisi "ingatan" sebagai kertas buram. Contoh operasi penetapan tersebut ada di bawah.
Untuk konsepsi yang lain dari apa yang membentuk sebuah algoritma lihat pemrograman fungsional dan pemrograman logika.
Menggambarkan algoritma[sunting | sunting sumber]
Algoritma dapat digambarkan dengan banyak notasi, termasuk bahasa alamiah, pseudokode, diagram alur, bagan drakon, bahasa pemrograman atau tabel kontrol (diproses oleh penerjemah). Ekspresi bahasa alamiah terhadap algoritma condong lebih banyak dan rancu, dan jarang digunakan untuk algoritma yang kompleks dan teknis. Pseudokode, diagram alur, bagan drakon, dan tabel kontrol adalah cara yang terstruktur untuk menggambarkan algoritma yang mencegah banyaknya kerancuan pada pernyataan-pernyataan bahasa alamiah. Bahasa pemrograman ditujukan untuk mengekspresikan algoritma dalam sebuah bentuk yang dapat dieksekusi oleh komputer, tapi sering kali digunakan sebagai suatu cara untuk menentukan atau mendokumentasikan algoritma.
Ada banyak macam kemungkinan representasi dan seseorang dapat mengekspresikan sebuah program mesin Turing sebagai urutan dari tabel-tabel mesin (lihat lebih lanjut dimesin kondisi-terbatas, tabel transisi kondisi dan tabel kontrol), sebagai diagram alur dan bagan drakon (lihat lebih lanjut di diagram kondisi), atau sebagai bentuk kode mesinatau kode assembly dasar yang dikenal "kumpulan lipat empat" (lihat lebih lanjut di mesin Turing).
Representasi dari algoritma dapat dikelompokan ke dalam tiga tingkatan dari deskripsi mesin Turing: [23]
- 1 Deskripsi tingkat-tinggi
- "... ditujukan untuk menjelaskan algoritma, menghiraukan rincian implementasi. Pada tingkat ini kita tidak perlu menyebutkan bagaimana mesin mengatur perangkat pita atau kepala pita rekam."
- 2 Deskripsi implementasi
- "... digunakan untuk menjelaskan cara mesin Turing menggunakan kepalanya dan cara menyimpan data. Pada tingkat ini kita tidak memberikan secara rinci kondisi atau fungsi transisi."
- 3 Deskripsi formal
- Lebih rinci, "tingkat paling rendah", menjelaskan "tabel kondisi" dari mesin Turing.
Sebagai contoh dari algoritma sederhana "Penjumlahan m+n" dijelaskan dalam tiga tingkatan tersebut lihat contoh algoritma.
Implementasi[sunting | sunting sumber]
Kebanyakan algoritma ditujukan untuk diimplementasikan sebagai program komputer. Namun, algoritma juga diimplementasikan dengan tujuan lain, seperti dalam jaringan sarafbiologis (sebagai contohnya, otak manusia yang mengimplementasikan aritmatika atau sebuah serangga yang melihat makanan), dalam sirkuit elektris, atau dalam sebuah perangkat mekanis.
Algoritma komputer[sunting | sunting sumber]
Dalam sistem komputer, sebuah algoritma pada dasarnya adalah instansi dari logika ditulis dalam perangkat lunak oleh pengembang perangkat lunak supaya efektif untuk komputer yang "ditargetkan" untuk mesin tertentu untuk menghasilkan keluaran dari masukan yang diberikan (kemungkinan nul).
Program yang "elegan" (padat), program yang "baik" (cepat): Pernyataan dari "sederhana dan elegan" muncul secara informal dalam buku Knuth dan dalam Chaitin:
- Knuth: "... kita menginginkan algoritma yang baik dalam definisi estetika sederhana. Salah satu kriterianya ... adalah waktu yang dibutuhkan untuk berjalannya algoritma ... Kriteria yang lain adalah adaptasi dari algoritma ke komputer, kesederhanaan dan elegan, dll" [24]
- Chaitin: "... sebuah program adalah 'elegan, maksud saya adalah ia merupakan program terkecil untuk menghasilkan keluaran." [25]
Chaitin membuka definisinya dengan: "Saya akan perlihatkan bahwa anda tidak dapat membuktikan sebuah program adalah 'elegan'" -- bukti tersebut akan menyelesaikan permasalahan perhentian (ibid).
Algoritma terhadap fungsi yang dapat dihitung oleh algoritma: Untuk sebuah fungsi bisa ada beberapa algoritma. Hal ini benar, bahkan tanpa mengembangkan kumpulan instruksi yang ada bagi programmer. Rogers mengamati bahwa "Sangat ... penting untuk membedakan antara pengertian algoritma, misalnya prosedur dan pernyataan fungsi yang dihitung oleh algoritma, misalnya pemetaan hasil dari prosedur. Fungsi yang sama bisa memiliki beberapa algoritma berbeda". [26]
Sayangnya ada pertukaran antara kebaikan (kecepatan) dan elegan (kepadatan) -- sebuah program yang elegan bisa melakukan lebih banyak langkah untuk menyelesaikan sebuah komputasi daripada yang kurang elegan. Sebuah contoh yang menggunakan algoritma Euclid bisa dilihat di bawah.
Komputer (dan komputor), model dari komputasi: Sebuah komputer (atau manusia "komputor" [27] ) adalah tipe terbatas dari mesin, sebuah "perangkat mekanis deterministik diskrit" [28] yang secara buta mengikuti instruksinya [29]. Model primitif dari Melzak dan Lambek [30] mereduksi pemikiran tersebut menjadi empat elemen: (i) diskrit, lokasi yang bisa dibedakan, (ii) diskrit, penghitung yang tak bisa dibedakan [31] (iii) sebuah agen, dan (iv) sebuah daftar instruksi yang efektif relatif terhadap kemampuan dari agen. [32]
Minsky menjelaskan variasi yang lebih sesuai dari model "abacus"-nya Lambek dalam "Basis Komputabilitas Paling Sederhana". [33] Mesin Minsky memproses secara berurutan lewat lima (atau enam tergantung bagaimana seseorang menghitungnya) instruksi kecuali baik sebuah kondisi IF-THEN GOTO atau GOTO tak bersyarat mengubah alur program keluar dari urutan. Selain HALT, mesin Minsky mengikutkan tiga operasi penetapan (penggantian, substitusi): [34] ZERO (misalnya, isi dari lokasi diganti oleh 0: L ← 0), SUCCESSOR (misalnya, L ← L+1), dan DECREMENT (misalnya, L ← L-1). [35] Jarang seorang programer harus menulis "kode" dengan kumpulan instruksi terbatas. Tapi Minsky memperlihatkan (sebagaimana Melzak dan Lambek) bahwa mesinnya adalah Turing komplit dengan hanya empat tipe instruksi utama: GOTO kondisional, GOTO tak bersyarat, penetapan/penggantian/substitusi, dan HALT. [36]
Simulasi dari sebuah algoritma: bahasa komputer (komputor): Knuth menganjurkan pembaca bahwa "cara terbaik untuk belajar algoritma dalah mencobanya ... langsung ambil pulpen dan kertas dan bekerja lewat contoh". [37] Lalu bagaimana dengan simulasi atau eksekusi yang sebenarnya? Programmer harus menerjemahkan algoritma ke dalam bahasa yang mana simulator/komputer/komputor dapat mengeksekusi secara efektif. Stone memberikan contoh dari hal ini: saat menghitung akar dari persamaan kuadrat si komputor harus tahu bagaimana mendapatkan akar kuadrat. Jika tidak maka supaya algoritma dapat efektif ia harus menyediakan sejumlah aturan untuk mengekstrak akar kuadrat. [38]
Hal ini berarti programer harus tahu sebuah "bahasa" yang efektif relatif terhadap target pada agen komputasi (komputer/komputor).
Lalu model apa yang seharusnya digunakan untuk simulasi? Van Emde Boas mengamati "bahkan bila kita mendasari teori kompleksitas dengan mesin abstrak bukannya mesin kongkrit, kesembarangan dari pemilihan model masih tetap ada. Pada titik itulah mulainya pemikiran simulasi". [39] Bila kecepatan yang dihitung, jumlah instruksi berpengaruh. Sebagai contohnya, subprogram dalam algoritma Euclid untuk menghitung sisa akan berjalan lebih cepat jika programmer memiliki instruksi "modulus" (sisa pembagian) bukannya dengan pengurangan (atau lebih parah: hanya "penurunan").
Pemrograman terstuktur, struktur kanonikal: Menurut Tesis Church-Turing setiap algoritma bisa dihitung dengan sebuah model yang dikenal Turing komplit, dan menurut demonstrasi Minsky kekomplitan Turing membutuhkan hanya empat tipe instruksi -- GOTO bersyarat, GOTO tak bersyarat, penetapan, HALT. Kemeny dan Kurtz mengamati bahwa saat penggunaan GOTO tak bersyarat yang "tak disiplin" dan IF-THEN GOTO bersyarat bisa menghasilkan "kode spageti" seorang programer bisa menulis program terstruktur menggunakan instruksi tersebut; di lain sisi "juga memungkinkan, dan tidak begitu sulit, untuk menulis sebuah program terstruktur yang buruk dalam sebuah bahasa terstruktur". [40] Tausworthe menambahkan tiga struktur kanon Bohm-Jacopini: [41] SEQUENCE, IF-THEN-ELSE, dan WHILE-DO, dengan dua lagi: DO-WHILE dan CASE. [42]Keuntungan dari program terstruktur adalah ia cocok dengan pembuktian kebenaran menggunakan induksi matematika. [43]
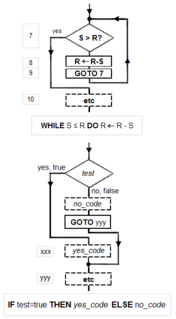
Simbol diagram alur [44]: Pembantu grafik yang disebut diagram alur memberikan suatu cara untuk menjelaskan dan mendokumentasikan sebuah algoritma (dan program komputer). Seperti alur program dari mesin Minsky, sebuah diagram alur selalu mulai dari atas dan terus ke bawah. Simbol utamanya hanya 4: arah panah memperlihatkan alur program, segi empat (SEQUENCE, GOTO), wajik (IF-THEN-ELSE), dan titik (OR). Struktur kanonikal Bohm-Jacopini dibuat dari bentuk-bentuk primitif tersebut. Sub-struktur bisa "bersarang" dalam segi empat hanya jika jalan keluar tunggal terjadi pada super-struktur. Simbol dan penggunaannya untuk membangun struktur kanonikal diperlihatkan dalam diagram.
Contoh[sunting | sunting sumber]
Info lebih lanjut: Contoh algoritma
Contoh Algoritma[sunting | sunting sumber]
Salah satu dari algoritma sederhana adalah menemukan bilangan terbesar dalam sebuah deretan angka (tak berurut). Solusinya membutuhkan pemeriksaan setiap angka dalam deret, tapi hanya sekali. Dari hal ini munculah algoritma sederhana, yang bisa dinyatakan dalam kalimat bahasa deskripsi tingkat-tinggi, sebagai:
Deskripsi tingkat-tinggi:
- Jika tidak ada angka dalam deret makan tidak ada bilangan terbesar.
- Asumsikan item pertama dalam deret adalah yang terbesar.
- Untuk setiap sisa angka dalam deret, jika angka tersebut besar dari angka terbesar sekarang, anggap angka tersebut menjadi yang terbesar dalam deret.
- Bila tidak ada lagi angka yang tersisa pada deret untuk diperiksa, anggap angka terbesar sekarang menjadi angka yang terbesar dalam deret.
Deskripsi (Quasi-)formal: Ditulis dalam kalimat yang lebih dekat dengan bahasa tingkat-tinggi dari program komputer, berikut ini adalah kode formal dari algoritma dalam pseudokode atau kode pijin:
Algoritma LargestNumber Masukan: Deret angka L. Keluaran: Angka terbesar dalam daftar L.
terbesar ← Lnull
untuk setiap item dalam L, lakukan
jika item > terbesar, maka
terbesar ← item
kembalikan terbesar
- "←" adalah singkatan untuk "diubah menjadi". Misalnya, "terbesar ← item" artinya nilai dari terbesar diubah menjadi nilai dari item.
- "kembalikan" mengakhiri algoritma dan mengeluarkan nilai kembalian.
Algoritma Euclid[sunting | sunting sumber]
Info lebih lanjut: Algoritma Euklid
Algoritma Euclid muncul sebagai Proposisi II dalam Book VII ("Elementary Number Theory") dari Elements. [45] Euclid mengajukan permasalahan: "Ambil dua angka bukan prima, untuk mencari bilangan pembagi terbesar". Dia menentukan "Sebuah angka [merupakan] besaran yang terdiri dari unit-unit": angka penghitung, integer positif kecuali 0. Dan "mengukur" adalah menempatkan ukuran panjang terkecil s dengan tepat (q kali) diantara ukuran terpanjang l sampai sisa r lebih kecil dari panjang terkecil s. [46]Dalam dunia modern, sisa r = l - q*s, q sebagai hasil bagi, atau sisa r adalah "modulus", bagian sisa-integer yang tersisa setelah pembagian. [47]
Supaya metode Euclid berhasil, panjang awalnya harus memenuhi dua kebutuhan: (i) panjangnya tidak 0, DAN (ii) hasil pengurangan harus "lebih", sebuah pengujian harus menjamin bahwa bilangan terkecil dari dua angka adalah hasil pengurangan dari yang terbesar (cara lain, keduanya bisa sama sehingga pengurangan menghasilkan 0).
Pembuktian asli Euclid mengikutkan kebutuhan yang ketiga: kedua panjang bukanlah bilangan prima. Euclid menentukan hal ini supaya dia bisa membentuk sebuah bukti reductio ad absurdum bahwa dua pembagi dua angka adalah yang terbesar. [48] Walau algoritma Nicomachus sama dengan Euclid, bila kedua bilangan prima maka menghasilkan angka "1" untuk bilangan pembagi terbesar. Jadi untuk lebih jelasnya algoritma berikut adalah algoritma Nicomachus.
Contoh[sunting | sunting sumber]
Bahasa komputer untuk algoritma Euclid[sunting | sunting sumber]
Hanya beberapa tipe instruksi yang dibutuhkan untuk mengeksekusi algoritma -- beberapa tes logika (GOTO bersyarat), GOTO tak bersyarat, penetapan (penggantian), dan pengurangan.
- Sebuah lokasi disimbolkan dengan huruf besar, misalnya, S, A, dll.
- Kuantitas beragam (angka) dalam sebuah lokasi ditulis dengan huruf kecil dan (biasanya) dihubungkan dengan nama lokasi. Sebagai contohnya, lokasi L pada awal bisa mengandung angka l = 3009.
Program yang kurang elegan (inelegan) untuk algoritma Euclid[sunting | sunting sumber]
Algoritma berikut disebut sebagai versi Euclid dan Nichomachus 4-langkah-nya Knuth, tapi bukannya menggunakan pembagi untuk menentukan sisa ia menggunakan pengurangan berturut-turut dari panjang terkecil s dari sisa panjang r sampai r kurang dari s. Deskripsi tingkat-tinggi, diperlihatkan dengan tulisan tebal, diadaptasi dari Knuth 1973:2-4:
INPUT:
1 [Kedalam dua lokasi L dan S taruh angka l dan s yang merepresentasikan kedua panjang]: INPUT L, S 2 [Inisialisasi R: buat supaya sisa panjang r sama dengan panjang awal l] R ← L
E0: [Pastikan r ≥ s.]
3 [Pastikan angka terkecil dari kedua angka ada dalam S dan yang terbesar di R]: IF R > S THEN isi dari L adalah angka terbesar jadi lewati langkah 4, 5 dan 6: GOTO step 6 ELSE tukar isi R dan S. 4 L ← R (langkah pertama ini berlebih, tapi berguna untuk diskusi nanti). 5 R ← S 6 S ← L
E1: [Cari sisa]: Sampai sisa panjang r di R kurang dari panjang terkecil s pada S, kurangi angka s dalam S berulang kali dari sisa panjang r dalam R.
7 IF S > R THEN selesai mengukur jadi GOTO 10 ELSE ukur lagi, 8 R ← R - S 9 [Pengulangan-sisa]: GOTO 7.
E2: [Apakah sisa 0?]: APAKAH (i) pengukuran terakhir adalah sama dan sisa di R adalah 0 program dapat berhenti, ATAU (ii) algoritma harus terus jalan: hasil pengukuran meninggalkan sisa di R kurang dari angka pengukuran dalam S.
10 IF R = 0 THEN selesai jadi GOTO langkah 15 ELSE lanjut ke langkah 11,
E3: [Interchange s dan r]: Sulitnya algoritma Euclid. Menggunakan sisa r untuk mengukur angka terkecil sebelumnya s:; L sebagai lokasi sementara.
11 L ← S 12 R ← S 13 S ← L 14 [Ulang proses pengukuran]: GOTO 7
OUTPUT:
15 [Selesai. S berisi faktor persekutuan terbesar]:
PRINT S
DONE:
16 HALT, END, STOP.
Program elegan untuk algoritma Euclid[sunting | sunting sumber]
Versi algoritma Euclid berikut hanya membutuhkan 6 instruksi inti untuk melakukan 13 langkah pada solusi "inelegan"; parahnya, "inelegan" membutuhkan tipe instruksi lebih banyak. Diagram alur dari "elegan" bisa dilihat pada bagian atas artikel ini. Dalam bahasa Basic (tak terstruktur) langkahnya diberi nomor, dan instruksi LET [] = [] adalah instruksi penetapan disimbolkan dengan ←.
5 REM Algoritma Euclid untuk faktor persekuturan terbesar 6 PRINT "Masukan dua integer besar dari 0" 10 INPUT A,B 20 IF B=0 THEN GOTO 80 30 IF A > B THEN GOTO 60 40 LET B=B-A 50 GOTO 20 60 LET A=A-B 70 GOTO 20 80 PRINT A 90 END
Bagaimana cara kerja "Elegan": Sebagai pengganti "pengulangan Euclid" luar, "Elegan" mengulang antara dua pengulangan, pengulangan A > B yang menghitung A ← A - B, dan pengualang B ≤ A yang menghitung B ← B - A. Hal ini bekerja karena, saat yang dikurang M lebih kecil pengurang S ( Selisih = pengurang - yang_di_kurang ), yang_dikurang bisa menjadi s (panjang pengukuran yang baru) dan pengurang bisa menjadi r yang baru (panjang yang akan diukur); dengan kata lain "arti" dari pengurangan dibalik.
Menguji algoritma Euclid[sunting | sunting sumber]
Apakah algoritma berjalan seperti yang penulis inginkan? Beberapa kasus uji cukup menentukan fungsi inti. Sumber pertama [49] menggunakan 3009 dan 884. Knuth menyarankan 40902, 24140. Kasus menarik lainnya yaitu dua angka relatif prima 14157 dan 5950.
Tapi kasus pengecualian harus teridentifikasi dan diuji. Apakah "inelegan" berjalan benar saat R > S, S > R, R = S? Sama juga dengan "Elegan": B > A, A > B, A = B? (Semuanya benar). Apa yang terjadi bila salah satu bilangan nol, atau keduanya nol? ("Inelegan" terus berjalan pada kedua kasus; "elegan" terus berjalan saat A = 0.) Apa yang terjadi bila angka negatif dimasukan? Angka desimal? Bila angka masukan, misalnya domain dari fungsi yang dihitung oleh algoritma/program, mengikutkan hanya integer positif termasuk 0, maka kegagalan pada nol mengindikasikan bahwa algoritma (dan program instansiasinya) adalah sebuah fungsi parsial bukannya fungsi total. Kesalahan yang terkenal karena eksepsi adalah kegagalan roket Ariane V.
Bukti dari kebenaran program menggunakan induksi matematika: Knuth mendemonstrasikan penggunaan induksi matematika untuk versi "pengembangan" dari algoritma Euclid, dan dia mengajukan "metode umum yang digunakan untuk membuktikan validitas dari setiap algoritma." [50] Tausworthe mengajukan bahwa sebuah pengukuran dari kompleksitas dari sebuah program adalah panjang dari pembuktian kebenarannya. [51]
Menghitung dan meningkatkan algoritma Euclid[sunting | sunting sumber]
Elegan (kepadatan) lawan kebaikan (kecepatan): Dengan hanya 6 instruksi dasar, "Elegan" adalah jelas pemenang dibandingkan dengan instruksi "inelegan" dengan 13 instruksi. Namun, "inelegan" lebih cepat (ia sampai pada HALT dengan langkah lebih sedikit). Analisis algoritma [52] mengindikasikan kenapa hal tersebut terjadi: "Elegan" melakukan pengujian kondisi dua kali disetiap pengulangan pengurangan, sementara "inelegan" hanya sekali. Bila algoritma (biasanya) membutuhkan banyak pengulangan,secara rata-rata lebih banyak waktu yang terbuang saat melakukan tes "B = 0?" yang hanya diperlukan saat sisa sudah dihitung.
Bisakah algoritma ditingkatkan?: Bila programmer sudah menilai sebuah program "cocok" dan "efektif" -- yaitu, ia menghitung fungsi yang ditujukan oleh penulisnya -- maka pertanyaannya menjadi, bisakah ditingkatkan?
Kepadatan dari "inelegan" bisa ditingkatkan dengan menghilangkan 5 langkah. Tapi Chaitin membuktikan bahwa memadatkan algoritma tidak bisa diotomatiskan dengan algoritma generalisasi; [53] tapi, ia bisa dilakukan secara heuristik, misalnya dengan pencarian menyeluruh (contohnya bisa ditemukan di Berang sibuk), coba dan gagal, kecerdasan, kedalaman, penggunaan penalaran induktif, dll. Bisa diamati bahwa langkah 4, 5, dan 6 diulang pada langkah 11, 12, dan 13. Pembandingan dengan "Elegan" menyediakan petunjuk langkah-langkah tersebut dengan langkah 2 dan 3 dapat dihilangkan. Hal ini mereduksi jumlah instruksi dasar dari 13 menjadi 8, yang membuatnya "lebih elegan" dari "Elegan" dengan 9 langkah.
Kecepatan "Elegan" bisa ditingkatkan dengan memindahkan tes B=0? keluar dari pengulangan. Perubahan ini memerlukan penambahan 3 instruksi (B=0?, A=0?, GOTO). Sekarang "Elegant" menghitung contoh-angka lebih cepat; untuk setiap angka pada A, B dan R, S hal ini selalu merupakan kasus yang membutuhkan analisis yang mendalam.
Sumber : wikipedia.com







Komentar
Posting Komentar